
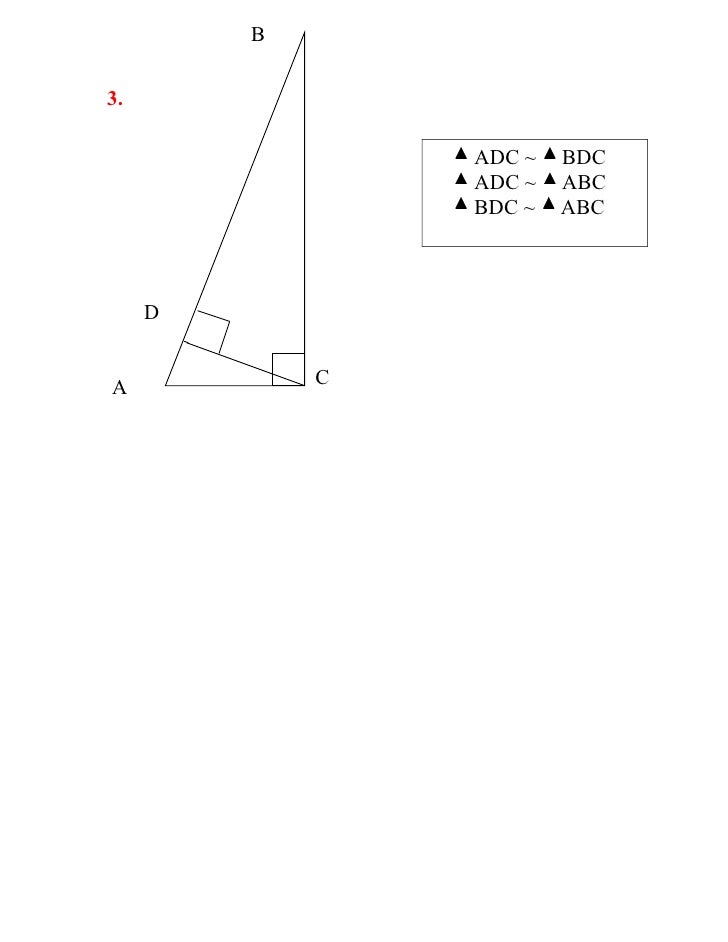

Go to and search about compass and straightedge construction. The length of the altitude is the geometric mean of the lengths of the segments of the hypotenuse. Using compass and straightedge, what kind of line segments can we construct?Ħ. Use compass and straightedge to constructĥ. Given three line segments of length $r$, $r a$ and $r b$. Use trigonometry to prove the Right Triangle Altitude Theorem.Ĥ. Write about your favourite example of similar triangles.ģ. This activity was designed for students who have been introduced to the geometric mean and have practiced re-drawing the three triangles formed by the altitude. The length of the altitude is the geometric mean of the. Prove that if two triangles have two pairs of equal angles then all their three pairs of angles are equal.Ģ. You may want to sketch the three right triangles to help you out. We will see the reason why the Right Triangle Altitude Theorem makes it possible for this construction. Hope to see you again then.ġ. In the next post, we will explore Gauss' construction of a regular 17-polygon. So indeed, the big square $CAIJ$ has area equal to the sum of two smaller squares $ABXY$ and $BCPQ$, and we have obtained the Pythagorean Theorem. In geometry, the altitude is a line that passes through two very specific points on a triangle: a vertex, or corner of a triangle, and its opposite side at a right, or 90-degree, angle. The right identity $CB^2 = CH \times CA = CH \times CJ$ shows that the square $BCPQ$ has the same area as the rectangle $CHMJ$.Using the left identity $AB^2 = AH \times AC = AH \times AI$, we can see that the square $ABXY$ has the same area as the rectangle $AHMI$. The right triangle altitude theorem or geometric mean theorem is a result in elementary geometry that describes a relation between the altitude on the.to the hypotenuse of a right triangle, including the geometric mean, to solve problems. Pythagorean Theorem says that the two squares $ABXY$ and $BCPQ$ have a total area equal to the big square $CAIJ$. Texas Geometry Standards Similarity, proof, and trigonometry. The altitude to the hypotenuse of a right triangle is the mean proportional between the segments into which it divides the hypotenuse. This entry was posted in Geometry and tagged geometric mean, geometric mean and right triangle, right triangle altitude theorem, right triangle altitude theorem proof, similar triangles, similarity proof by Math Proofs.

In right ABC shown above, altitude CD is drawn to the hypotenuse, forming two smaller right triangles they are. The vertices are at the points (0,0), (0,8), and (6,0). Using a Geometric Mean To Solve Problems. These prove the Right Triangle Altitude Theorem. Directions: The black triangle is a right triangle with legs 8 and 6. Given sides a and b find side c and the perimeter, semiperimeter, area and altitudes. The geometric mean of two positive integers $latex a$ and $latex b$ is $latex \sqrt$. Altitude c of Right Triangle: hc (a b) / c.


 0 kommentar(er)
0 kommentar(er)
